

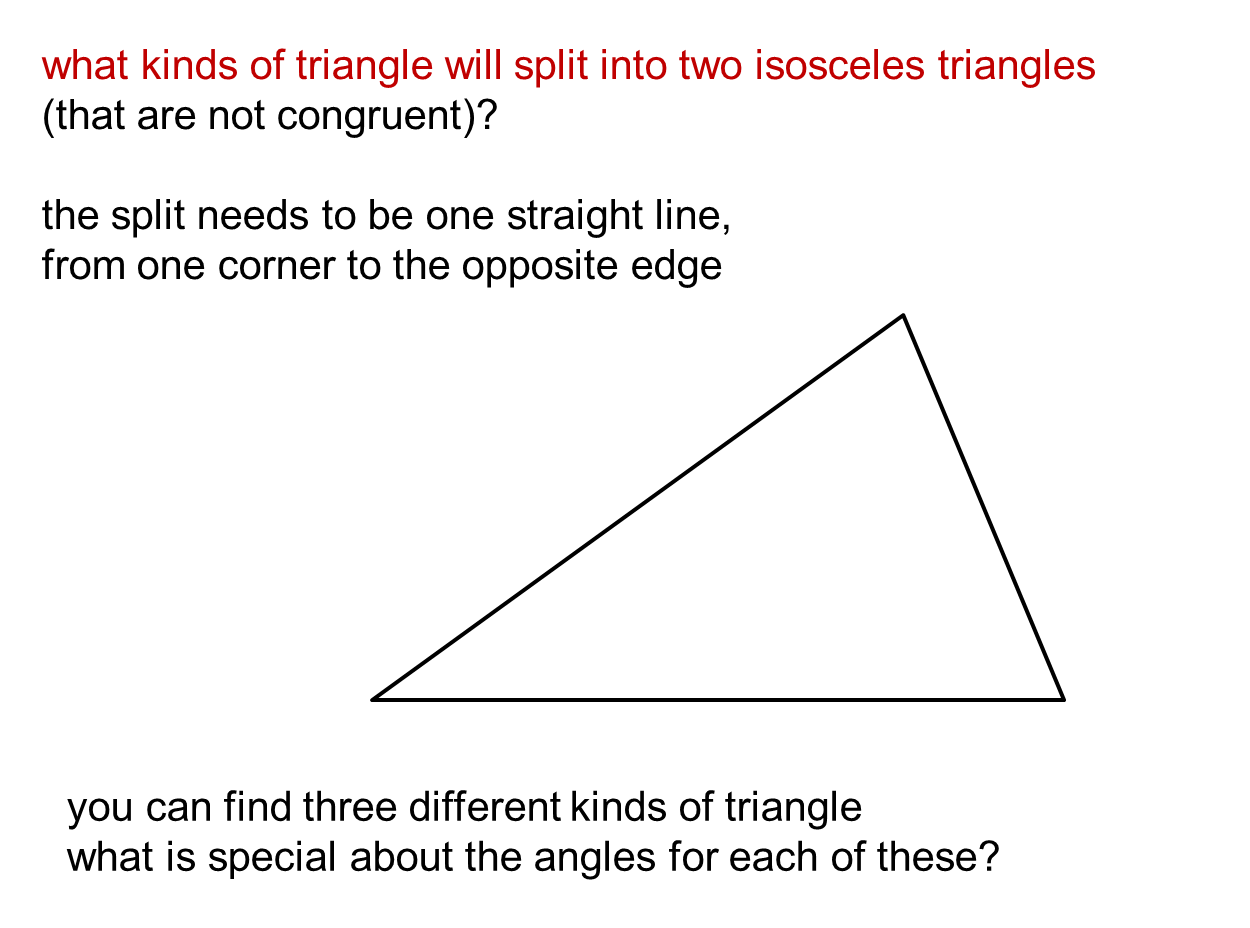
Since we know that X = Z because it is an isosceles triangle, then we can solve for the measures of all the angles. First we read "The degree measure of a base angle", so let's start with X= triangle logo are trademarks of JUSTIN Vineyards & Winery LLC, Paso Robles. An isosceles triangle is a triangle with two sides of equal length and two equal internal angles adjacent to each equal sides. We need to make an equation out of this problem, so let's figure out what it's trying to tell us. JUSTIN, EXCEPTIONAL FROM EVERY ANGLE, ISOSCELES, SAVANT, RIGHT ANGLE. Notice that it's hard to draw a picture without knowing which angles are largest. Find the degree measure of the vertex angle Y. The degree measure of a base angle of isosceles triangle XYZ exceeds three times the degrees measure of the vertex Y by 60. The measure of vertex angle S in triangle RST is 52 degrees. Find the degree measure of the vertex angle S.īase angle + base angle + vertex angle S = 180 degreesĦ4 degrees + 64 degrees + x = 180 degrees Base angles R and T both measure 64 degrees. In isosceles triangle RST, angle S is the vertex angle. (1) Let x = the measure of each base angle.īase angle + base angle + 120 degrees = 180 degreesĮach base angle of triangle ABC measures 30 degrees. Find the degree measure of each base angle. The vertex angle B of isosceles triangle ABC is 120 degrees. The angle located opposite the base is called the vertex. In an isosceles triangle, we have two sides called the legs and a third side called the base. The easiest way to define an isosceles triangle is that it has two equal sides. Similarly, if two angles of a triangle have equal measure, then the sides opposite those angles are the same length. Theorem 2.5.1 means that if AC BC in ABC then A B. If two sides of a triangle are equal the angles opposite these sides are equal. In an isosceles triangle, the base angles have the same degree measure and are, as a result, equal (congruent). The most important fact about isosceles triangles is the following: Theorem 2.5.1. There is a special triangle called an isosceles triangle. If and only if one pair of internal angles of two triangles have the same measure as each other, and another pair also have the same measure as each other, the triangles are similar.There are many types of triangles in the world of geometry. Are All Triangles Isosceles Euclids great synthesis of Greek geometry, The Elements, was for centuries regarded as a model of abstract axiomatic reasoning.Some basic theorems about similar triangles are: The corresponding sides of similar triangles have lengths that are in the same proportion, and this property is also sufficient to establish similarity. Two triangles are said to be similar, if every angle of one triangle has the same measure as the corresponding angle in the other triangle. The sum of the measures of the three exterior angles (one for each vertex) of any triangle is 360 degrees. The measure of an exterior angle of a triangle is equal to the sum of the measures of the two interior angles that are not adjacent to it this is the exterior angle theorem. An exterior angle of a triangle is an angle that is a linear pair (and hence supplementary) to an interior angle. This allows determination of the measure of the third angle of any triangle, given the measure of two angles. This fact is equivalent to Euclid's parallel postulate. The sum of the measures of the interior angles of a triangle in Euclidean space is always 180 degrees. The measures of the interior angles of the triangle always add up to 180 degrees (same color to point out they are equal).
Elementary facts about triangles were presented by Euclid, in books 1–4 of his Elements, written around 300 BC. In rigorous treatments, a triangle is therefore called a 2- simplex (see also Polytope). Triangles are assumed to be two- dimensional plane figures, unless the context provides otherwise (see § Non-planar triangles, below).

A triangle with vertices A, B, and C is denoted △ A B C īasic facts A triangle, showing exterior angle d. It is one of the basic shapes in geometry. A triangle is a polygon with three edges and three vertices.


 0 kommentar(er)
0 kommentar(er)
